形式·空间·算法:一年级形态构成课程教学实验
2024.01-25
2023年秋季学期后8周的构成设计课程,是一年级本科生第一个以个人设计训练为目的的设计课程。本教学实验首次引入了参数化设计方法,以引导学生更好地理解由实体元素和虚体空间所构成的形式背后所存在着的明确、清晰的逻辑关系,辅导学生以设计概念、逻辑为底层核心去发展自己的构成设计。参数化教学实验小组(后文简称参数化小组)包含8名一年级建筑学本科同学,由韩孟臻、冬木千枝两位教师,杨有有、芶静怡两位助教指导教学。1教学目标及课程结构
经多年教学实践,清华大学建筑系的形态构成教学已形成鲜明的教学目标与方法,即:通过设计辅导,让学生掌握对抽象实体要素与虚体空间的形式操作方法,并理解有意味的形式背后蕴含着明晰的秩序法则。实验教学遵循同样的教学目标,绝非以最终炫酷的曲面形式为目的,而是希望通过grasshopper的程序化方式,更加透彻地提炼形式、空间背后的秩序法则(在此亦即算法逻辑)。① 算法思维,是希望学生通过自定义的算法,强调学生对于控制着最终形态的设计逻辑的建立与阐释。将原本头脑中的设计逻辑,以程序的方式梳理表达。② 跨学科性,则体现在设计过程中所涉及到的,来自不同系统的知识,如几何学、仿生学等。借此理解美的形式的来源,及其背后的控制规则。教学共分为三个教学阶段:首先是软件入门与基础参数化技能培养;其次是相关的理论知识讲解与实际案例的应用练习;最终是设计阶段,学生通过探索不同系统的组合,创造出新颖的实体要素和虚体空间形态。2 各阶段教学内容
2.1 技能培养——参数化设计工具训练
本阶段教学重点是参数化设计技能的培养。同学们通过课前预讲解、课堂辅导及课后练习,熟悉并掌握Rhino和Grasshopper建模的基本操作。其中的重点是帮助学生理解 Grasshopper参数化建模的基本原理,为后续学习打下基础。2.2 理论与应用——“系统”工具的引入
本阶段教学聚焦于“系统”(system)这一设计工具。同学们学习如何以Grasshopper为媒介,将来自不同学科的各种系统运用在概念构思与设计深化中。课程共带领同学们探索了三个系统:场(field)、聚合(aggregation)和泰森多边形(Voronoi)。教学方式均由教师讲解引入,随后通过若干小案例建模练习加以巩固,最后让学生自由运用所学系统完成一个设计小作业。该阶段学习也有利于学生理解系统是如何影响实际建筑形式设计的。2.3 方案设计——形态构成设计
作为课程的核心阶段,同学们将所学系统应用到各自的设计之中,探索实体要素和虚体空间的构成关系。学生首先须清晰地定义其设计目标,随后寻找合适的算法逻辑,将目标充分表达,形成最终设计方案。设计过程并非是线性的;而是在教师与助教的指导下,通过讨论设计概念、构思原型、检验算法可行性、评估结果、优化调整等一系列步骤达成设计目标,最终形成兼具算法与形式美感的设计作品。在这一反复迭代的动态设计教学过程中,培养训练了学生将设计意图、操作手法和设计结果等要素关联起来的能力。3 课程设计成果
3.1 打破边界
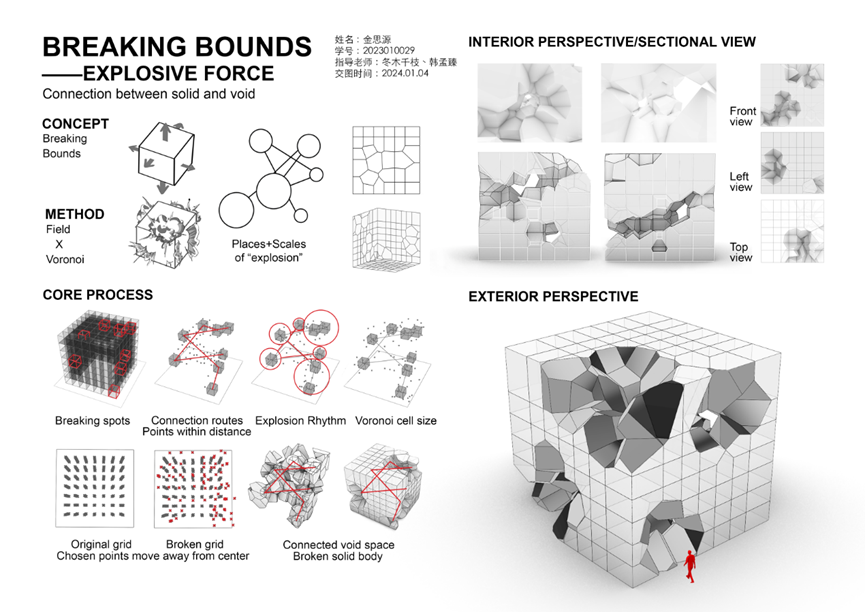
BREAKING BOUNDARIES
作者:金思源
本构成作品的设计概念是“打破边界”。作者意图塑造一个贯通边界的、联通的空间,从立方体中破茧而出,以表现”打破“所具有的力量感。在具体形式操作上,作者针对基础三维方格网的顶点进行了基于力场系统的操作,利用泰森多面体创造出一个联通的变异形态空间,进而通过材质对比(半透明的基础网格vs金属反射的泰森多面体表面),强化虚实与形态的差异性,表现空间对于基本网格边界的突破。
3.2 扭曲与拓扑学
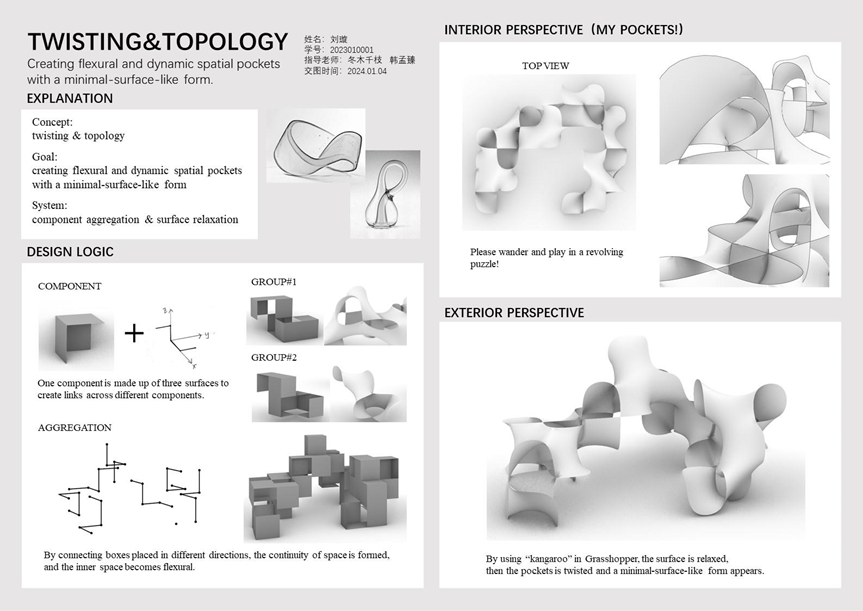
TWISTING & TOPOLOGY
作者:刘璇
作者对于扭曲、旋转、有动感的内部空间感兴趣。Twisting描述了空间的特质,Topology则意味着对空间关系的关注。作者首先通过单元聚合,将由立方体变形而成的基本单元旋转、组合,围合出不断变化方向的空间。之后再利用算法“化方成圆”,将原先由矩形拼接而成的外表面变换为连续曲面,以获得内部空间的扭曲感和流动感。最终作品在要素与空间两个方面都呈现出蜿蜒、流动的形式。3.3 连贯与整体
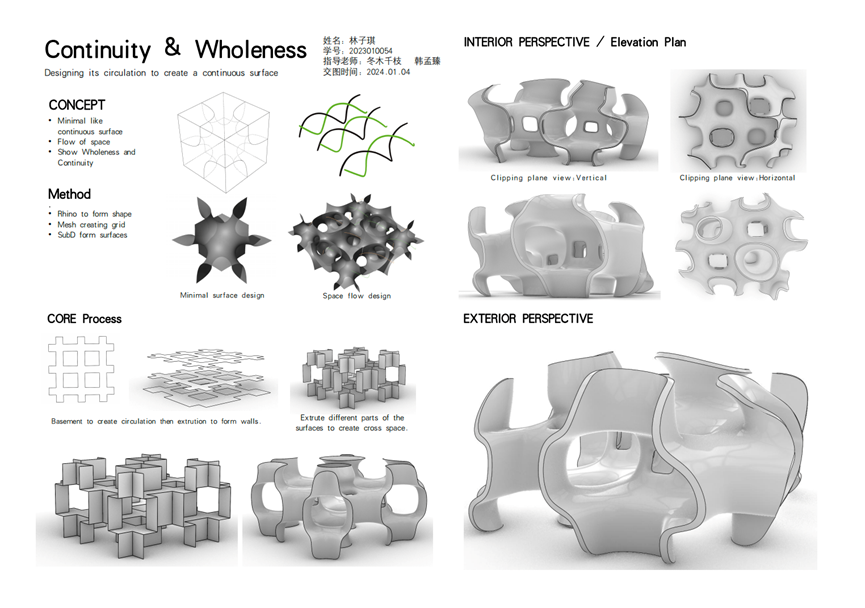
CONTINUITY & WHOLENESS
作者:林子琪
作者意图使用连续曲面创造兼具连贯性与整体性的空间。连贯性(Continuity)描述了空间的形态关系;整体性(Wholeness)则描述了空间内部的体验感。在具体操作上,作者通过Rhino建模的方式先创造出平面,再利用同一平面挤出不同部分形成层与层之间的空间穿插,之后使用SubD塑造出最终的连续的曲面实体,同时该曲面也围合、包裹出具有流动性的、相互穿插的空间形态。
3.4 律动穿插
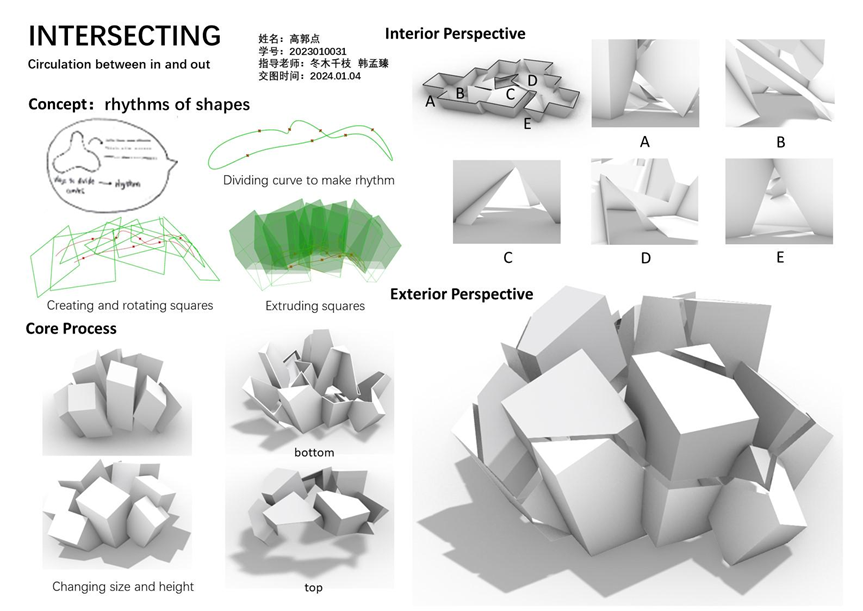
RHYTHMS OF INTERSECTING,
作者:高郭点
本构成设计希望表现“音乐的律动”。设计出发于三维曲线上所分布的7个点,根据它们距离中心点的距离远近,定义生成7个大小、高度、角度各异的长方体,穿插组合在一起。在去除长方体相互叠合部分,形成内部连续的空间之后;进一步基于流线与视线的连续性,对整体进行了切割与赋材,达成了最终表现律动、穿插的设计作品。
3.5 内外贯通
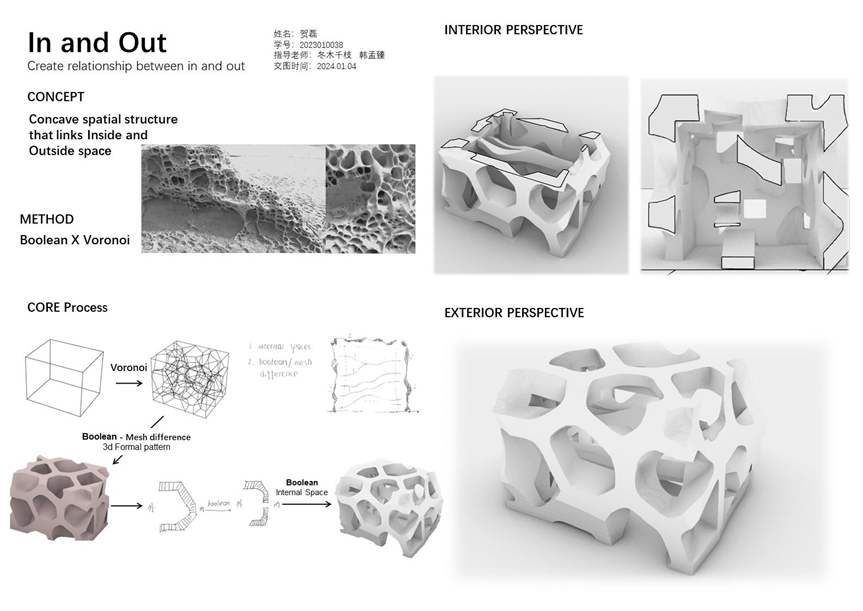
IN & OUT,
作者:贺磊
作者意图通过塑造一个内外贯通的空间,让原本被体量表皮隔绝的内外空间建立联系。在形式操作上,作者利用泰森多面体与布尔运算在立方体的表面上创造出一个个如同风化形成的凹陷与坑洞。体量表面因而从有厚度的平面,转变为具备了进深的空间。内部空间中具有流动感的结构,进一步强化出内外空间的联通关系。
3.6 跨层连接
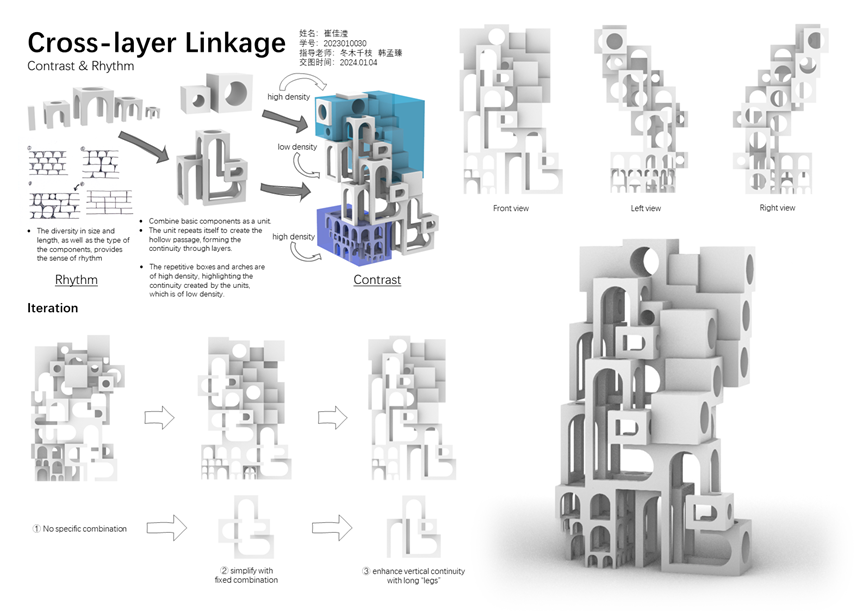
CROSS-LAYER LINKAGE
作者:崔佳滢
本构成作品的设计概念是“跨层连接”。作者意图塑造实体与空间两个层面的连续,具有“层”的限定但超越“层”的桎梏,表达自由与动感。作者采用了带有拱圈形态的基本单元,以重复的手法组合构造出在竖直维度的连续性。进而,通过不同尺度大小的基本单元组合,形成密度变化的层次,借助疏密、虚实的对比,强调跨层连接的空间。3.7 流动曲面
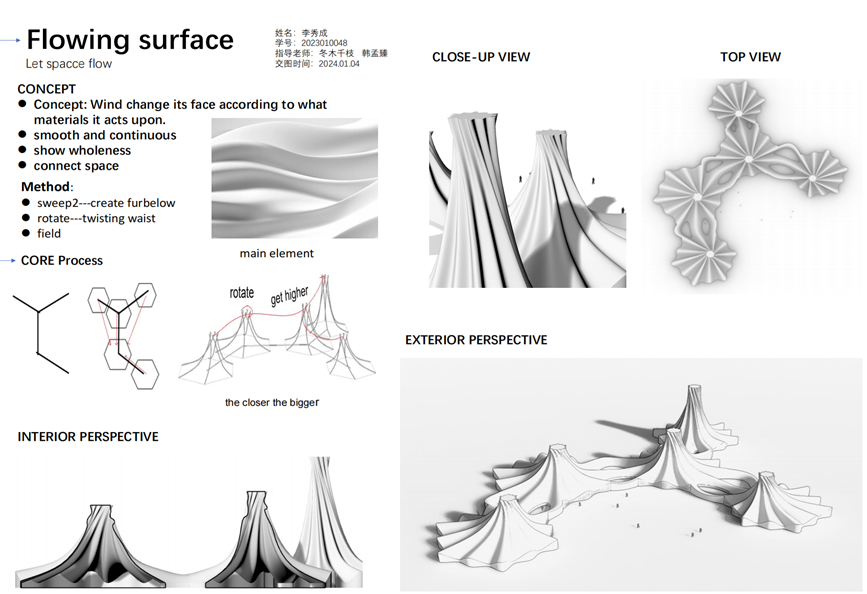
FLOWING SURFACE
作者:李秀成
设计者想要用流动曲面来构造空间,创造具有连续性的动态之美。设计灵感来源于少女翩翩起舞的长裙,灵动而有活力。作者先构造六边形基底,向上用nurbs曲线形成框架,sweept形成裙面。每个裙摆之间并非简单复制,而是彼此通过光滑的曲面相连,构成一个有机的整体。裙摆上部的微微扭转,仿佛是少女扭动的腰部,绽放活力。
3.8 小径分岔
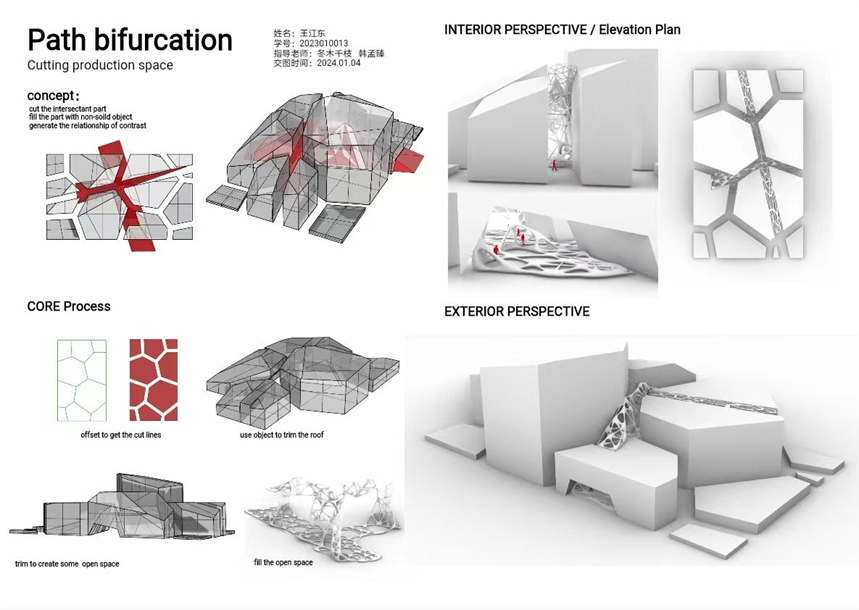
PATH BIFURCATION
作者:王江东
设计名称源于博尔赫斯的小说,“小径分岔”意味着一种对空间的选择。作为基础,实体体块之间的间隙形成了诸多分岔的巷道形空间;进而通过人为切削,塑造更具三维体验感的半开放管道型空间;最后以镂空网格表皮标识人为切削而出的空间,与原本的缝隙空间加以区分,形成主次关系。经过8周高强度的教学与练习,我们欣喜地发现,除了软件技术,同学们均在一定程度上理解了运算思维和参数化方法在设计中的应用,理解了形式生成背后所须的秩序法则,这都将成为同学们未来设计思维发展的种子。除了感谢冬木千枝老师,杨有有、芶静怡助教的辛勤付出,还须感谢8位同学的热情投入和程晓喜副院长的大力支持。